Аэродинамические сопротивления

Движение реального потока дымовых газов и воздуха в котле представляет собой сложный случай турбулентного движения сжимаемой жидкости при неадиабатных условиях. В процессе движения потока газов и воздуха в газоходах и поверхностях нагрева котла изменяются температура, плотность и давление газа. В общем случае движение вязкой и теплопроводящей жидкости описывается уравнением Навье-Стокса, уравнением сплошности, уравнением переноса теплоты и термодинамическими уравнениями, характеризующими состояние среды и зависимость ее энтальпии от давления и температуры.

При малых перепадах давлений, малых скоростях установившегося движения и неизменной температуре продукты сгорания и воздух на элементарных участках газовоздушного тракта могут рассматриваться как идеальные, несжимаемые и невязкие газы. Тогда энергетический баланс для элементарной струи таких газов может быть выражен уравнением Бернулли

где z - геометрическая высота центра тяжести данного сечения потока; w²р/2-удельная кинетическая энергия потока на данном уровне, отнесенная к секундному массовому расходу; w -1 скорость потока; р - плотность потока; р - энергия давления или потенциальная энергия потока. Движение газов в газовоздушном тракте сопровождается потерей энергии, затрачиваемой на преодоление действия сил турбулентного трения потока газа о твердые поверхности и между слоями потока. На преодоление трения при движении потока необходимо располагать избыточным давлением, которое уменьшается по мере прохождения потока через данный элемент тракта. Падение давления потока идеального газа может быть определено из рассмотрения уравнений Бернулли для уровней I и II вертикального элемента тракта (рис. 11.2):

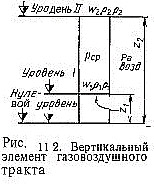
для уровня I

и для уровня II

где z₁ и z₂ - высоты уровней I и II относительно условного уровня от-счета; g - ускорение силы свободного падения; p₁ и р₂ - плотность потока на уровнях I и II; w₁ и w₂ - скорости потока на уровнях I и II. Принимая, что р₁ = р₂ = Р_со, и приравнивая левые части уравнений (25.2) и (25.3) с учетом сопротивления участка I-11-∆р, после группировки членов уравнения получаем

Правая часть уравнения представляет собой затрату потенциальной и кинетической энергии, расходуемой на преодоление трения и ускорение потока при движении его на участке I-II, определяющую перепад давления на этом участке. Исходя из приведенного уравнения в инженерной практике перепад полных давлений на участке тракта, Па, определяется по формуле

где р_п = w²р/2 - динамическое давление (скоростной напор), Па; p_ст= p-(р_о-p_azg)-статическое давление, т. е. разность между абсолютным давлением р на данном уровне 2 и абсолютным атмосферным давлением ро на том же уровне, Па; ∆р - сопротивление участка, Па; p_c=(z₂- z₁) (р_а-р) - самотяга, Па; р и р_а - плотности движущейся среды и атмосферного воздуха.

Физически самотяга объясняется тем, что подъем потока газа с начального уровня на некоторую высоту сопровождается опусканием такого же объема воздуха с этой высоты до начального уровня. В результате затрата работы на подъем газа сопровождается получением работы за счет опускания такого же объемного количества воздуха с той же высоты. При равных температурах газа и атмосферного воздуха затрата работы на подъем газа компенсируется работой, совершаемой при опускании воздуха, и результативная работа равна нулю. Если температура газа выше температуры атмосферного воздуха и плотность его ниже, чем у воздуха, то работа, затрачиваемая на подъем газа, меньше работы, совершаемой при опускании того же объема воздуха, и избыточная работа может быть затрачена на преодоление сопротивлений движению газа.

Соответственно самотяга газового тракта, Па,

где L - высота подъема газа от начального до конечного уровня, м.

При движении газа вверх самотяга уменьшает полных давлений, при движении вниз - увеличивает. При равенстве плотностей газа и атмосферного воздуха, а также в горизонтальных газоходах самотяга равна нулю. Сопротивление, возникающее при движении потока газов, состоит из сопротивления трения при течении потока в прямом канале постоянного сечения, в том числе при продольном омывании пучка труб; местных сопротивлений, связанных с изменением формы или направления потока, которые условно считают сосредоточенными в одном сечении и не включающими аэродинамические сопротивление трения; аэродинамические сопротивления поперечно омываемых пучков труб, в которых раздельно сопротивление трения и местные аэродинамические сопротивления определить нельзя. Сопротивление трения пропорционально длине газохода, коэффициенту трения и кинетической энергии потока и обратно пропорционально сечению газохода. Местные аэродинамические сопротивления определяются геометрической конфигурацией участка газохода и пропорциональны кинетической энергии потока. Сопротивление трения для изотермического потока, т. е. при постоянной его плотности и вязкости, Па, определяется по формуле

где ʎ - коэффициент сопротивления трения, который зависит от относительной шероховатости стенок канала и числа Re; I, d_э - длина и эквивалентный диаметр канала, м; w - скорость потока, м/с; р - плотность газа, кг/м³.

При наличии теплообмена между потоком и ограничивающими его поверхностями плотность и вязкость газа изменяются по шероховатых труб в условиях теплообмена, Па, используется формула длине и сечению канала, в связи с чем в формулу (11.7) вносится температурная поправка. Для определения сопротивления трения

где Т_ст и Т - средние по участку газохода температуры стенки и текущей среды, К.

Значения К в зависимости от числа Re и относительной шероховатости стенок приведены в [2]. При ламинарном движении потока, когда Re<2-103, коэффициент сопротивления не зависит от шероховатости и определяется по формуле

Для технических гладких труб и значений Re=(4-b 100)-103 коэффициент сопротивления трения может определяться по формуле Блазиуса

Местное сопротивление, как указано выше, условно считается сосредоточенным в определенном сечении газохода; в действительности потеря энергии потока, вызванная изменением формы или направления газохода, происходит на относительно длинном участке газохода. Поэтому принято, что местное сопротивление представляет собой разность между фактической потерей энергии на этом участке и потерей, которая имела бы место от трения при неизменных форме и направлении газохода. Все местные аэродинамические сопротивления, в том числе и при наличии теплообмена, Па, определяются по формуле

где ξ - коэффициент местного аэродинамические сопротивления.

Значения ξ меняются в широких пределах в зависимости от конфигурации газохода. Для наиболее часто встречающихся типов местных сопротивлений значения I приведены в [2,6].
Сопротивление пучков труб при поперечном их омывании, при отсутствии и наличии теплообмена определяется по формуле

Значение коэффициента местного аэродинамические сопротивления в данном случае зависит от количества рядов труб, их расположения и числа Re. Скорость потока в формуле (11.12) опрееляется для самого сжатого сечения газохода. Для пучка с коридорным расположением труб

где z₂ - количество рядов труб по глубине пучка; ξ₀ - коэффициент аэродинамические сопротивления на один ряд труб, зависящий от величин s₁\d, s₁-d/s₂-d=ψ и от числа Re. Здесь s₁ и s₂ - шаги труб по ширине и глубине пучка, м; d - наружный диаметр труб, м.

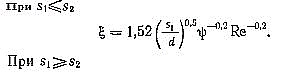
Для пучка с шахматным расположением труб

где z₂ - число рядов труб по глубине пучка;

где Cs - коэффициент формы пучка, зависящий от отношений -диагональный шаг труб, м.

Для шахматных пучков труб с S₁/d>2,0 Cs=3,2. Перепад полных давлений по газовому тракту, Па, при искусственной тяге определяется по формуле

где р" - разрежение на выходе из топки, обычно принимается около 20 Па; ∆р - суммарное сопротивление газового тракта без учета самотяги и поправки на запыленность газов, удельный вес газов и давление, Па; расчет этих поправок приведен в [2]; р_с - суммарная самотяга газового тракта с соответствующим знаком, Па.

Перепад полных давлений по воздушному тракту, Па, при искусственной тяге определяется по формуле

где р'_т =р"_т+0,95р' - разрежение в топке на уровне ввода воздуха в топку; здесь р' - перепад давлений между сечениями выхода газов из топки и ввода воздуха в топку, Па.
В формулах (11.14) и (11.15) при движении вверх знак «+», при движении вниз знак «-». В случае работы котла с наддувом перепад полных давлений в газовом и воздушном трактах, Па,

В поверхностях нагрева котла повышение скорости газов интенсифицирует конвективный теплообмен и коэффициент теплоотдачи от газов к стенке возрастает пропорционально скорости в степени 0,6-0,8. Соответственно уменьшаются необходимые поверхности нагрева при заданном их тепловосприятии.Аэродинамические сопротивления при движении потока газов возрастают пропорционально квадрату скорости, и соответственно увеличиваются расходы электроэнергии на тягу и дутье.

Выбор скорости потока газов определяется технико-экономическим расчетом. Оптимальная скорость, очевидно, будет при минимальных эксплуатационных затратах на поверхности нагрева и электроэнергии на тягу и дутье.

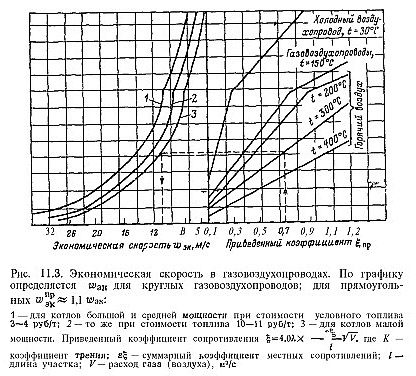
На рис. 11.3 показана номограмма для выбора скорости в воздухопроводах и газопроводах круглого сечения в зависимости от конструкции и приведенного коэффициента сопротивления воздуховода или газопровода; температуры газа или воздуха; стоимости электроэнергии. Для прямоугольных воздуховодов и газопроводов принимается увеличение на 10 % значений скорости, определенной по номограмме.

В котлах, работающих на пыли твердого топлива, повышение скорости газов лимитируется износом поверхностей нагрева, интенсивность которого в основном определяется содержанием уноса в газах и скоростью потока. Обычно в поверхностях нагрева при поперечном омывании их потоком газов скорость принимается w = 84-10 м/с. При продольном движении газов в трубах воздухоподогревателя w=10-г-14м/с.

В металлических газоходах, соединяющих элементы газовоздушного тракта, скорость потока принимается по конструктивным соображениям. В случаях движения горячих газов или воздуха обычно w= 10ч-14 м/с, холодных w - = 64-8 м/с. С целью уменьшения сопротивлений следует принимать меньшие значения скоростей потока, если это конструктивно возможно.